Ottimizzazione
Lo shader descritto nella prima parte calcola la sfocatura di ciascun pixel applicando la formula:
dove è il kernel gaussiano 2D, è il raggio e l’immagine da processare. La definizione implica che per ciascun pixel in output vengono letti pixel dall’immagine di input.
Graficando i tempi di esecuzione al variare della dimensione del kernel, emerge chiaramente un andamento quadratico:

Benchmark effetuato con scheda NVIDIA GeForce RTX 4080 Laptop GPU
In questo articolo vedremo come sfruttare una particolare proprietà del kernel gaussiano per calcolare in modo più efficiente.
#Kernel separabili
Un kernel si dice separabile se può essere espresso come il prodotto di due funzioni indipendenti tra loro:
Il kernel gaussiano gode di questa proprietà, infatti:
I fattori indipendenti e sono entrambi kernel Gaussiani 1D.
#Convoluzione discreta
Definiamo la convoluzione discreta di rispetto a come l’operatore:
Dato un kernel monodimensionale , definiamo la convoluzione parziale rispetto all’asse x (o convoluzione orizzontale) di rispetto a :
Analogamente, definiamo la convoluzione parziale rispetto all’asse y (o convoluzione verticale) di rispetto a :
#Convoluzione di kernel separabili
Il calcolo di equivale alla convoluzione discreta di con il kernel gaussiano :
Poichè il kernel gaussiano è separabile, possiamo riscrivere:
Il fattore è costante rispetto alla sommatoria interna, quindi possiamo portarlo all’esterno:
La sommatoria interna rappresenta il pixel della convoluzione verticale di rispetto a :
Sostituendo:
La sommatoria rimasta è la convoluzione orizzontale di rispetto al kernel :
La convoluzione completa è quindi equivalente a:
- Applicare una convoluzione verticale con il kernel .
- Successivamente, applicare una convoluzione orizzontale con il kernel (o viceversa, scambiando l’ordine delle sommatorie).
Poichè ciascuna convoluzione parziale ha complessità , il calcolo combinato ha complessità per pixel, ottenendo così un vantaggio significativo rispetto al calcolo diretto, che ha complessità per pixel.
#Implementazione
La versione ottimizzata del filtro gaussiano è implementata nella classe Gauss2dBlurOptimized, che mantiene la stessa
interfaccia di Gauss2dBlur. La differenza principale risiede nell’utilizzo di due passaggi distinti per applicare le
convoluzioni parziali, sfruttando una texture di lavoro intermedia.
#Texture di lavoro
Per gestire le due convoluzioni parziali, la classe utilizza una texture di lavoro intermedia, rappresentata dalla proprietà
privata workingTexture. La texture viene allocata e gestita dinamicamente in base alla dimensione della texture di input,
come illustrato nel seguente codice:
export class Gauss2dBlurOptimized { /* ...Same as Gauss2dBlur... */ private workingTexture: GPUTexture | undefined;
private ensureTextures( inputTexture: GPUTexture ) { if (this.needsRecreation(inputTexture)) { this.destroyTextures();
console.log("Creating textures..."); this.workingTexture = this.device.createTexture({ size: { width: inputTexture.width, height: inputTexture.height }, format: inputTexture.format, usage: GPUTextureUsage.RENDER_ATTACHMENT | GPUTextureUsage.TEXTURE_BINDING }); } }
private needsRecreation( inputTexture: GPUTexture ) { return !this.workingTexture || this.workingTexture.width < inputTexture.width || this.workingTexture.height < inputTexture.height; }
destroyTextures() { console.log("Destroying textures..."); this.workingTexture?.destroy(); }
destroy() { this.destroyTextures(); this.uniformBuffer?.destroy(); }}Il metodo ensureTextures() verifica se la texture di lavoro esistente è compatibile con la texture di input. In caso
contrario, dealloca quella precedente e ne crea una nuova. Il formato della texture di input non può cambiare senza ricreare
lo shader, quindi non viene tenuto in considerazione in needsRecreation().
La texture di lavoro viene distrutta con il metodo destroy() insieme alle altre risorse allocate, oppure in destroyTextures()
che può essere usato per liberare memoria senza invalidare la classe.
#Operazione di blur
A differenza della versione base, che calcola direttamente la convoluzione 2D in un unico passaggio, questa implementazione separa le due convoluzioni lungo gli assi, utilizzando la texture di lavoro per il passaggio intermedio. Il codice seguente illustra il processo:
export class Gauss2dBlurOptimized { static async create( device: GPUDevice, inputFormat: GPUTextureFormat, timer?: GPUTimer ) { /* ...Same as Gauss2dBlur... */
// Create uniform buffer for kernel size and blur direction const uniformBuffer = device.createBuffer({ size: 8, usage: GPUBufferUsage.UNIFORM | GPUBufferUsage.COPY_DST });
/* ...Same as Gauss2dBlur... */ }
async blur( inputTexture: GPUTexture, kernelRadius: number, outputTexture?: GPUTexture ): Promise<GPUTexture> { /* ...Same as Gauss2dBlur... */
// Ensure that working texture is usable this.ensureTextures(inputTexture);
// Perform two 1D pass blur this.gaussBlur1dPass( inputTexture, this.workingTexture!, kernelRadius, 0 ); this.gaussBlur1dPass( this.workingTexture!, outputTexture, kernelRadius, 1 );
return outputTexture; }
private gaussBlur1dPass( inputTex: GPUTexture, outTex: GPUTexture, kernelRadius: number, blurDirection: 0 | 1 ) { const commandEncoder = this.device.createCommandEncoder();
// Update the uniform buffer this.device.queue.writeBuffer( this.uniformBuffer!, 0, new Int32Array([ kernelRadius, blurDirection ]) );
/* ...Same as Gauss2dBlur... */ }}Nella prima passata, viene calcolata la convoluzione orizzontale (con blurDirection = 0), e il risultato viene salvato
nella texture di lavoro. Nella seconda passata, invece, si esegue la convoluzione verticale (con blurDirection = 1),
producendo l’immagine finale nella texture di output. Inoltre, il buffer uniforme, oltre al raggio del kernel, ora
include anche la direzione della sfocatura, che può essere orizzontale o verticale.
#Shader
Nel fragment shader, a seconda della direzione della convoluzione, viene chiamata la funzione blurW() o blurH() per
calcolare la convoluzione parziale. Queste funzioni generano il kernel di sfocatura gaussiana e applicano la convoluzione
nella direzione appropriata:
function gauss2dBlurShader(format: GPUTextureFormat): string { const formatInfo = TEXTURE_FORMAT_INFO[format]!;
// language=WGSL return ` ```wgsl /*... no changes ...*/
struct Params { kernelRadius: i32,
// 0 = W, 1 = H direction: i32 }
/*... no changes ...*/
fn blurW(coords: vec2i, stdDev: f32) -> ${formatInfo.texelType} { let norm = 1.0 / sqrt(2.0 * PI * stdDev * stdDev);
// Gaussian blur kernel generation var blur = ${castToFloat(formatInfo.texelType)}(0);
// Since we are discretizing the Gaussian kernel // the sum of the samples won't add up perfectly to 1 var weightSum = 0.0f;
for (var i = -params.kernelRadius; i <= params.kernelRadius; i++) { let weight = exp(-(f32(i * i) / (2.0 * stdDev * stdDev))); let I = textureLoad(inputTexture, coords + vec2i(i, 0), 0).${channelMask(formatInfo.channelsCount)}; let gij = norm * weight;
blur += ${castToFloat(formatInfo.texelType)}(I) * gij; weightSum += gij; }
// Normalize the result by dividing by the sum of the weights blur /= weightSum; ${formatInfo.channelsCount === 4 ? "blur.a = 1.0f;" : "" }
return ${formatInfo.texelType}(blur); }
fn blurH(coords: vec2i, stdDev: f32) -> ${formatInfo.texelType} { /*...similar to blurW ...*/ }
@fragment fn fs(@builtin(position) coord: vec4f) -> @location(0) ${formatInfo.texelType} { // 99% of Gaussian values fall within 3 * stdDev // P(mu - 3s <= X <= mu + 3s) = 0.9973 let stdDev = f32(params.kernelRadius) / 3.0;
// Gaussian blur kernel generation let pixelCoords = vec2i(coord.xy - 0.5); var blur: ${formatInfo.texelType}; if (params.direction == 0) { blur = blurW(pixelCoords, stdDev); } else { blur = blurH(pixelCoords, stdDev); }
return blur; } ``` `;}#Benchmarking
WebGPU offre una funzionalità chiamata timestamp queries per misurare con precisione i tempi di esecuzione sulla GPU.
Per utilizzarli, è necessario abilitare la feature timestamp-query al momento della richiesta del device:
const device = await adapter.requestDevice({ requiredFeatures: [ 'timestamp-query' ]});#Allocazione delle query
Per allocare una serie di timestamp queries, si utilizza il metodo createQuerySet():
const querySet = device.createQuerySet({ type: 'timestamp', count: 2});Per memorizzare i risultati delle query, è necessario allocare un buffer dedicato:
const resolveBuffer = device.createBuffer({ size: querySet.count * 8, usage: GPUBufferUsage.QUERY_RESOLVE | GPUBufferUsage.COPY_SRC});Il buffer deve supportare l’uso QUERY_RESOLVE, e ciascun timestamp occupa 8 byte (pari a un BigInt in JavaScript).
Per leggere i timestamp sulla CPU sarà necessario trasferire resolveBuffer in un buffer mappabile:
const stagingBuffer = device.createBuffer({ size: resolveBuffer.size, usage: GPUBufferUsage.COPY_DST | GPUBufferUsage.MAP_READ});#Configurazione delle query
Ogni render pass può registrare fino a due timestamp (inizio e fine), configurando il parametro timestampWrites al
momento della creazione:
const encoder = device.createCommandEncoder();const renderPass = encoder.beginRenderPass({ timestampWrites: { querySet, beginningOfPassWriteIndex: 0, endOfPassWriteIndex: 1 }});In questo esempio, il timestamp d’inizio viene salvato in querySet[0] mentre il timestamp di fine in querySet[1].
#Salvataggio dei timestamp
Dopo aver concluso la render pass, ma prima di chiamare finish() sul command encoder, è necessario utilizzare il metodo
resolveQuerySet() per scrivere i risultati nel buffer di destinazione:
// ...draw stuff...renderPass.end();encoder.resolveQuerySet( // queries querySet,
// first query 0,
// query count querySet.count,
// destination resolveBuffer,
// destination offset 0);#Lettura dei risultati
Per accedere ai dati sulla CPU, è necessario copiare il resolveBuffer sul buffer di staging:
encoder.copyBufferToBuffer( resolveBuffer,
// source offset 0,
stagingBuffer,
// destination offset 0,
stagingBuffer.size);
device.queue.submit([ commandEncoder.finish()]);A questo punto stagingBuffer è pronto per essere mappato sulla CPU:
try { await stagingBuffer.mapAsync(GPUMapMode.READ); const times = new BigInt64Array( this.stagingBuffer.getMappedRange() ); const elapsedMs = Number(times[1] - times[0]) * 1e-6;} finally { stagingBuffer.unmap();}I timestamp sono espressi in nanosecondi e le query possono essere riutilizzate, ma è fondamentale liberare le risorse quando non servono più:
resolveBuffer.destroy();stagingBuffer.destroy();querySet.destroy();#L’utility GPUTimer
La classe di utility GPUTimer semplifica l’utilizzo dei timestamp queries, e può essere usata nel seguente modo:
- Creare un oggetto timer dal device:
const timer = new GPUTimer(device);- Aggiungere il timer alla render pass:
const commandEncoder = device.createCommandEncoder();const renderPass = commandEncoder.beginRenderPass({ ...passDescriptor, // Adds timestamp measurements ...timer.renderPass});
// ...draw stuff...- Risolvere i query set prima del submit:
// ...draw stuff...renderPass.end();
timer.resolveQuerySet(commandEncoder);device.queue.submit([commandEncoder.finish()]);- Leggere la durata dopo il submit:
// Later, read the timing:const duration = await timer.read();console.log(`Operation took ${timer.fmtTime(duration)}`);- Rilasciare il timer quando non serve più:
timer.destroy();#Risultati finali
Con la nuova implementazione, il filtro gaussiano è applicato in due passate separate, ottimizzando così il processo:
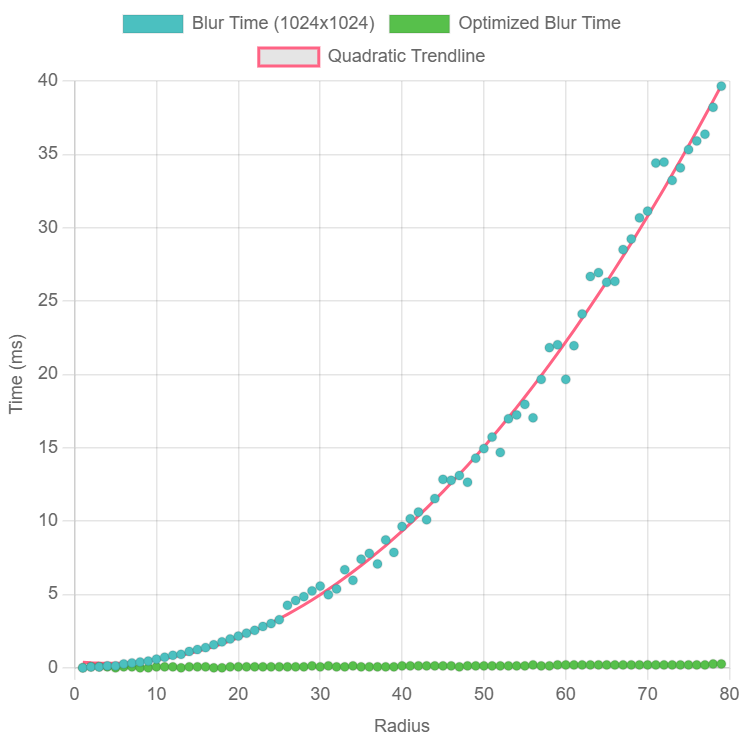
Benchmark effetuato con scheda NVIDIA GeForce RTX 4080 Laptop GPU
Come si può osservare, la nuova versione offre un vantaggio netto in termini di prestazioni, con un andamento lineare del tempo di esecuzione rispetto alla dimensione del kernel.
#Conclusioni e passi successivi
La convoluzione gaussiana, pur essendo computazionalmente intensiva nella sua forma diretta, può essere ottimizzata tramite la separabilità del kernel, riducendo la complessità computazionale da a .
L’efficacia dell’ottimizzazione è stata confermata attraverso misurazioni precise dei tempi di esecuzione, utilizzando le timestamp queries fornite da WebGPU.
Nella terza e ultima parte certificheremo correttezza e robustezza dell’implementazione attraverso la creazione di una suite di test unitari dedicata.
Stay tuned! 🚀